
100次浏览 发布时间:2024-11-01 10:34:01
日常我们购买电器类商品时我们都会关注一下这个电器功率、能效等级、直流、交流等相关的参数。一台电器从生产到出厂都会严格按照国家规定和标准进行生产,譬如在我们国家销售的家用电器必须满足在AC220V电压可以正常使用。当然还有很多国家的硬性指标保证家用电器的生产、使用安全。检测仪表有哪些硬性指标来确保其安全可靠性呢?
评价仪表的品质指标是多方面的,作为仪表的基本性能,主要是衡量仪表测量能力的那些指标,如、误差、精确度、稳定性、测量范围、输入输出特性等。
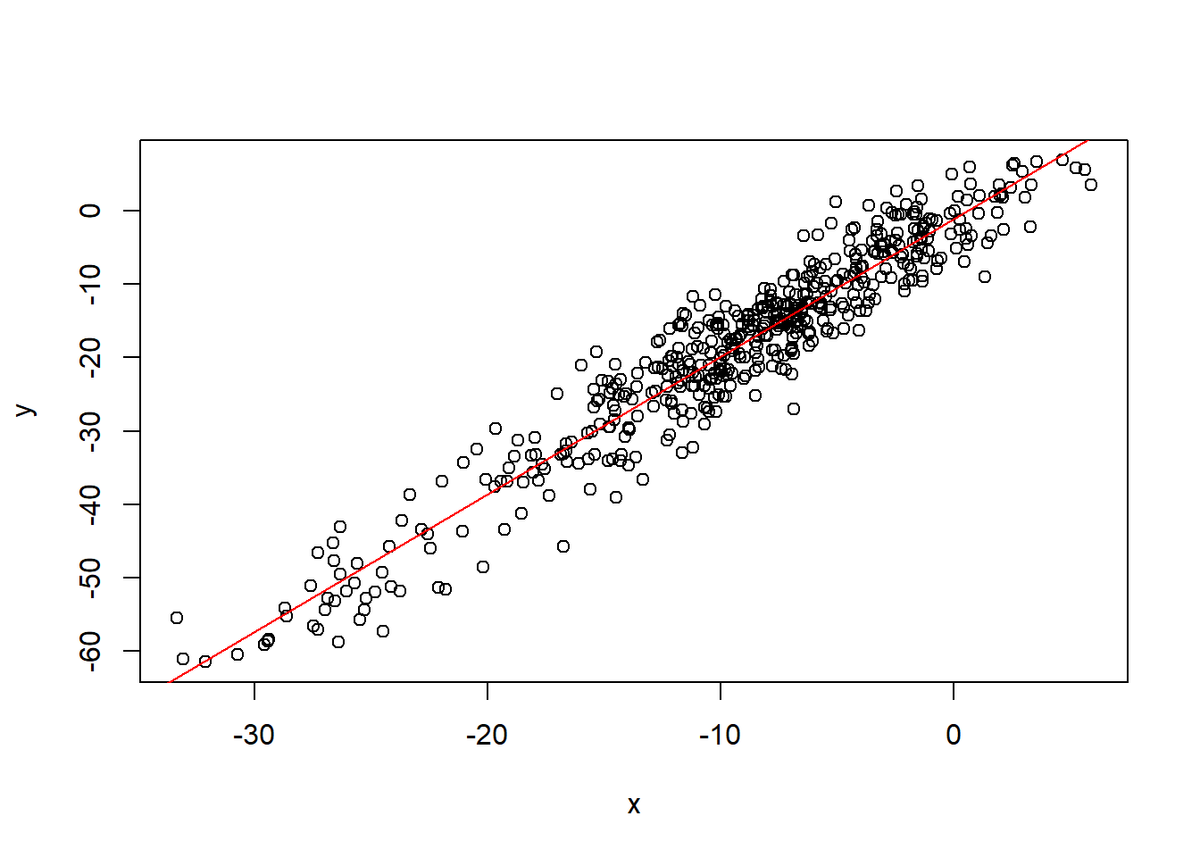
说明精确度的指标有三个:精密度、准确度和精确度。
精密度表示仪表指示值的分散程度。
准确度是指仪表的指示值(简称示值)偏离被测量真正值的程度。
精确度(简称精度)是精密度和准确度的综合反映。
三、稳定性
仪表的稳定性主要考虑两个方面的影响:稳定度和环境
稳定度是由于仪表内部某些随机变化的因素引起的。例如仪表内部某些因素周期性变化、飘移或机械部分的摩擦力变化等引起仪表的示值变化。通常它以精密度的数值和时间长短一起来表示。
环境影响使用仪表时的周围环境(如室温、湿度、大气压、震动等)条件变化引起仪表示值变化,以及电源电压、波形、频率等工作条件变化引起仪表示值变化,统称为环境影响,用影响系数表示。

四、基本技术指标
选取一台合适的仪表从工艺介质类型、压力、温度、周围环境考虑,处理考虑这些还需要考虑量程、误差、精度等仪表本身的指标。
仪表能够测量的最大输入量与最小输入量之间的范围称作仪表的量程范围,简称量程。
在数值上等于仪表上限值与下限值的代数差之绝对值。
例如:某台压力表的最低指示-10kpa,最高指示120kpa,它的量程就是120kpa。量程范围就是-10kpa到120kpa。
量程上下限的选择:
仪表量程的上限:Ymax: 4/3~3/2倍(被测变量)
波动较大时:3/2~2倍(被测变量)
下限:一般地,被测变量的值不低于全量程的1/3。

在稳定情况下,仪表输出变化量△L与引起此变化的输入量的变化量△Xb之比值,定义为仪表的灵敏度。
用S表示,即式中,
S—— 仪表灵敏度
△L、△Xb—— 分别为输入与输出变化量
例如:某测量范围是0~100℃的温度表,其满量程时指针转角为270度,它的灵敏度是2.7度/℃。
3、灵敏限也叫分辨率或死区
它表明仪表响应输入量微小变化的能力指标,即不能引起输出发生变化的最大输入变化幅度与量程范围之比的百分数。
4、基本误差
仪表测量值中的最大示值绝对误差Δm与仪表量程Lm之比值称为仪表的基本误差σj。
5、允许误差
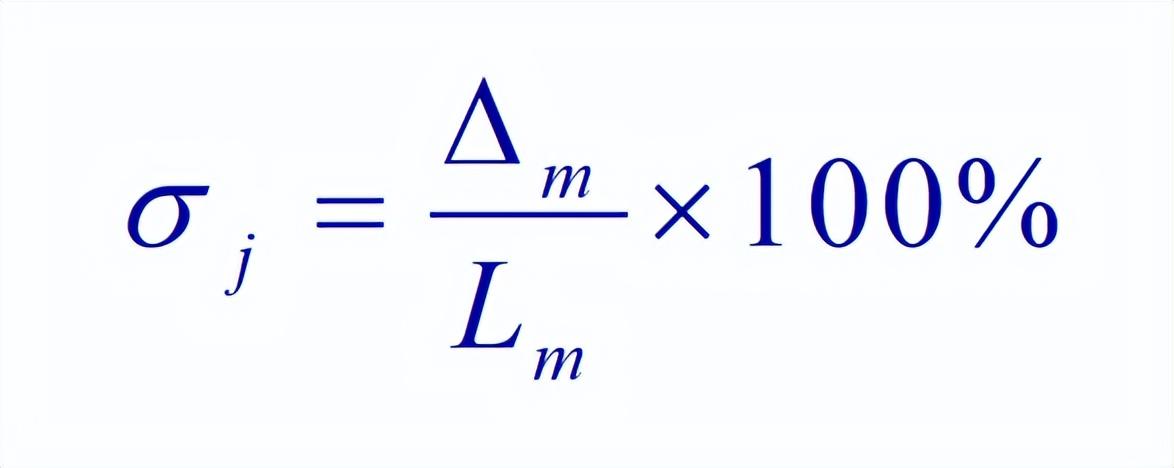
它表示对测量仪表所允许的误差界限,即出厂的仪表都要保证基本误差不超过某一规定值,此规定值叫允许误差。
仪表的δ允越大,表示它的精确度越低;反之,仪表的δ允越小,表示仪表的精确度越高。

它指根据测量仪表准确度大小所划分的等级或级别。允许误差去掉百分号的数值就是准确度等级,工程上称为精度等级。
目前常用的精确度等级有0.005,0.02,0.05,0.1,0.2,0.4,0.5,1.0,1.5,2.5,4.0等。
国家标准序列: 标准表、范型表、实用表。可参考《GBT 13283-2008工业过程测量和控制用检测仪表和显示仪表精确度等级》
Ⅰ级标准表:0.005、0.02、0.05 ;
Ⅱ级标准表:0.1 、0.2 、0.35 、0.5 ;
一般标准表:1.0 、1.5、2.5 、4.0。
精度等级一般用一定的符号形式表示在仪表面板上或铭牌上:

仪表的精度等级是衡量仪表质量优劣的重要指标之一。
精度等级数值越小,表示仪表的精确度越高。
精度等级数值小于等于0.05的仪表通常用来作为标准表,而工业用表的精度等级数值一般大于等于0.5。
仪表精度与量程有关,量程是根据所要测量的工艺变量来确定的。在仪表精度等级一定的前提下适当缩小量程,可以减小测量误差,提高测量准确性。
仪表投用以后除了仪表本身的误差影响外,受人为因素或环境因素还会产生误差叫测量误差。
1、观测误差
当对某观测量进行观测,其观测值与真值(客观存在或理论值)之差,称为测量误差。
用数学式子表达: △i = Li – X (i=1,2…n) L —观测值 X—真值
测量误差的产生主要有三个方面:
①仪器原因:仪器结构、制造方面,每一种仪器具有一定的精确度,因而使观测结果的精确度受到一定限制。
②人为原因:观测者感官鉴别能力有一定的局限性。观测者的习惯因素、工作态度、技术熟练程度等也会给观测者的成果带来不同程度的影响。
③环境原因:
例如:外界环境如温度、湿度、风力、大气折光等因素的变化,均使观测结果产生误差。
例如:温度变化使钢尺产生伸缩阳光曝晒使水准气泡偏移,大气折光使望远镜的瞄准产生偏差,风力过大使仪器安置不稳定等。
人、仪器和外界环境通常称为观测条件;
观测条件相同的各次观测称为等精度观测;
观测条件不相同的各次观测称为不等精度观测。
2、测量误差
先作两个前提假设:
① 观测条件相同.
② 对某一量进行一系列的直接观测在此基础上分析出现的误差的数值 、符号及变化规律。
例子一:用理论长度为10米而实际长度为10.04米的钢尺测量距离。统计结果如下:
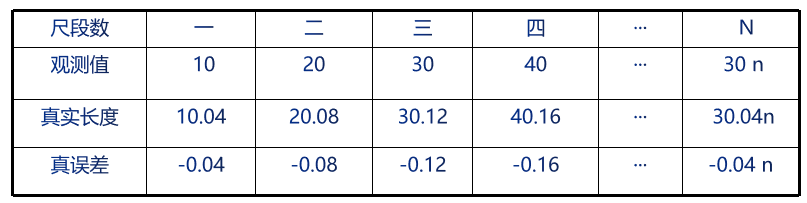
通过例子一表格发现了规律:
①误差符号始终不变,具有规律性。
②误差大小与所量直线成 正比,具有累积性。
③误差对观测结果的危害性很大。
例子二、在厘米的水准尺上估读毫米时,有时估读过大,有时估过小,每次估读也不可能绝对相等,其影响大小,纯属偶然。
通过例子二发现了规律:
① 从个别误差来考察,其符号、数值始终变化,无任何规律性。
② 多次重复观测,取其平均数,可抵消一些误差的影响。
我们将这些误差归结为:
①系统误差:在相同的观测条件下,对某一量进行一系列的观测,如果出现的误差在符号和数值上都相同,或按一定的规律变化,这种误差称为“系统误差”。 系统误差具有规律性。
②偶然误差:在相同的观测条件下,对某一量进行一系列的观测,如果误差出现的符号和数值大小都不相同,从表面上看没有任何规律性,为种误差称为“偶然误差”。个别偶然误差虽无规律,但大量的偶然误差具有统计规律。
③粗差:观测中的错误叫粗差。
例如:读错、记错、算错、瞄错目标等。错误是观测者疏大意造成的,观测结果中不允许有错误。一旦发现,应及时更正或重测。
在观测过程中,系统误差和偶然误差总是同时产生。
系统误差对观测结果的影响尤为显著,应尽可能地加以改正、抵消或削弱。对可能存在的情况不明的系统误差,可采用不同时间的多次观测,消弱其影响。
消除系统误差的常用的有效方法:
① 检校仪器:使系统误差降低到最小程度。
② 求改正数:将观测值加以改正,消除其影响。
③ 采用合理的观测方法:如对向观测。
消除或削弱偶然误差的有效方法:
系统误差对观测结果的影响显著,应尽可能地加以改正、抵消或削弱。对情况不明的系统误差,采用不同时间的多次观测。