偏导数怎么求（直观了解偏导数与全导数）

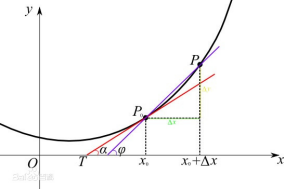
当函数有一个自变量时，比如y=f(x)，是一个一元函数，在直角坐标系中表示f(x)几何图形就是一条线，我们求导就是求切线，目的是利用切线段代替曲线来求曲线的长度，也就是利用直线段代替曲线段做计算，为什么呢?是因为人们只会测量直线段的长度。

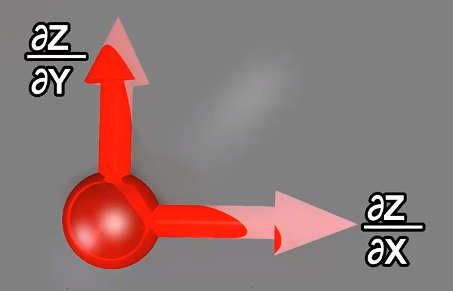
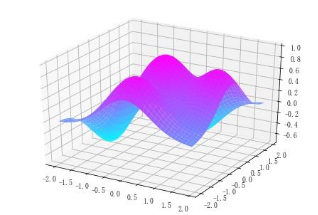
当函数含有多个自变量时，比如z=f(x,y)，是一个二元函数，在直角坐标系中表示f(x,y)几何图形就是一个面，那我们怎么处理呢？人们只能把曲面切成曲线，曲线切成直线段，进行计算。曲面切成曲线的过程就是求偏导数的过程，偏导数就是求一维曲线，目的是利用曲线段代替曲面。比如我们下图，我们对y求偏导，就是把x看成常数，取值某点x,其结果就是沿着y轴变化的曲线，当x取值变化时，y的偏导也跟随变化，x值取所有范围，y的偏导曲线也就组成了曲面。

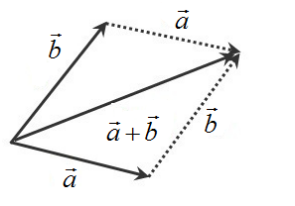
同理我们也可以用同样的方式对x取偏导；偏导都是有方向的直线段，当我们在一点即对x取偏导，又对y取偏导时，他们有各自的方向和大小，如果我们按照矢量的运算进行求和，得出结果就是对函数对x,y,的全导数。全导数就是对所有自变量求导再取他们合力结果，也就是每个变量对函数的影响之和。